Se llama forma de onda a la trayectoria trazada por una magnitud, dibujada en función de una variable (tiempo, grado, radianes, etc.) de una fuerza electromotriz, una corriente o una potencia eléctrica.
Las formas de onda más comunes son:
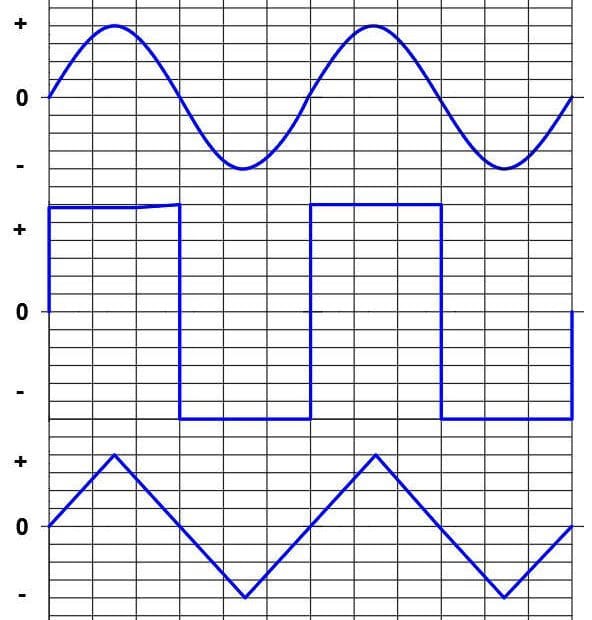
a) senoidal;
b) cuadrada;
c) triangular;
Mostradas en la imagen de arriba.
La onda más usual en corriente alterna es la senoidal. Se caracteriza por sus alternancias positivas y negativas en el tiempo.
Una onda senoidal de fem produce ondas, también senoidal de corriente y potencia.
Elementos de una onda senoidal
Los elementos de una onda senoidal son:
a) Valor instantáneo: es el tamaño que una forma de onda alcanza en cualquier instante. Se denota por medio de minúsculas, e, u, i, w, e=Emax sen Q.
b) Amplitud o valor pico: es el valor máximo de una forma de onda, se indica con mayúsculas, Emax, Ep, Ιmax x Ιp.
c) Período: es el tiempo que una onda periódica tarda en realizar un ciclo. Intervalo de tiempo entre repeticiones sucesivas de una forma de onda periódica. Se denota con la letra T y se mide en segundos. T=1/f. Es el inverso de la frecuencia.
d) Ciclo: es la porción de una forma de onda contenida en un periodo.

T1 = T2 = T3. Ciclo o porción de onda contenida en un periodo.
f) frecuencia: es el número da ciclos que se producen en un segundo; se representa con la letra f y se mide en ciclos sobre segundo, f=c/s.
La frecuencia y el periodo son inversos o recíprocos f=1/T y T=1/f.
La unidad de frecuencia es el Hertz (Hz). Se tiene una frecuencia de 1 Hz cuando se realiza un ciclo en un segundo.

f ) Alternancia positiva o cresta: es la porción de la forma de onda que aparece por arriba del eje horizontal.
g) Alternancia negativa o valle: es la porción de forma de onda que aparece por abajo del eje horizontal.
h) Longitud de onda: es la distancia entre dos puntos simétricos de una onda. Distancia entre el inicio y el final de un ciclo. Se representa con la letra griega lambda (λ) y se mide en metros.

a = valor instantáneo.
b = valor máximo, valor pico o amplitud.
c = alternancia positiva.
d = alternancia negativa.
e = longitud de onda.
f = final del ciclo
o = origen del ciclo.
La longitud de onda puede determinarse con la siguiente expresión: λ = e/f;
e = velocidad de la luz y f = frecuencia de la onda.
Se tiene una onda de corriente alterna con frecuencia de 60 Hz y 5 amperes de valor máximo. Determinar:
a) Su periodo: T = 1 / f = 1 / 60 = 0.0166 segundos.
b) Su longitud de onda: λ = e/f = 3*10^8 / 60 = 5*10^6 m
c) Su amplitud o valor pico de la corriente:
Ap = Amax = amplitud = 5 amperes.
El valor instantáneo de una onda senoidal se determina con la expresión:
v = Vmax sen φ, para una fem de corriente alterna.
i = Imax sen φ, para una corriente alterna.
Como:

v = Vmax sen wt ó i = Imax sen wt
Pero:

v = Vmax sen 2π f t ó i = Imax sen 2π f t
Una onda senoidal se puede acotar a lo largo del eje horizontal en: grados, radianes o en segundos.

Cuando se conoce el periodo, se pueden determinar los segundos correspondientes a cada punto de referencia, dados en grados o en radianes.
Relación entre radianes y grados
2π radianes = 360° ; 1 radian = 360/2π = 57.3° = 180/π
Para convertir grados a radianes
Radianes = (π/180) * grados
Ejemplo: Convertir 30° a radianes
Radianes = (π/180) * 30 = 0.524
Para convertir radianes a grados
Grados = (180/π) * radianes
Convertir 0.524 radianes a grados
Grados = (180/π) * 0.524 = 30°
Ejercicios de onda senoidal
1. Una onda senoidal tiene una frecuencia de 60 Hz. Determinar en qué tiempo alcanza su valor pico o valor máximo. Se puede observar que el valor máximo en su alternancia positiva lo alcanza en un cuarto de ciclo, luego:

Es el tiempo en que la onda avanza 90° o π/2 radianes.
2. Calcular el valor instantáneo de una corriente alterna de valor pico o máximo de 5 A, cuando la onda haya alcanzado 30°.
i = Imax sen φ ; i = 5 sen 30° = 2.5 A.
3. Calcular el valor instantáneo de una onda de 60 Hz con valor pico o máximo de 5 volts, transcurridos 1.39 ms.
v = Vmax sen wt = Vm sen 2π f t
f = 60 Hz
t = 1.39*10^-3
w = 2 π f = 2π * 60 = 377 radianes/s
Para poder manejar la función seno, es necesario transformar los radianes a grados. Así:
Grados = (180/π) * 377 = 21,600.5° al multiplicar los grados por 1.39*10^-3 resultan = 30°
Finalmente resulta que v = 5 sen 30° = 2.5 volts.
Valor medio y valor eficaz
En ondas senoidales se manejan dos términos o conceptos llamados valor medio y valor eficaz.
El valor medio del área comprendida por la alternancia positiva queda dada por la expresión:
Vmed = (2/π) * Vp = 0.636 Vp y Vp = (π/2) * Vmed = 1.57 Vm
El valor promedio de un ciclo completo es cero, puesto que se tiene una alternancia positiva y otra idéntica negativa. Sin embargo, si se considera sólo la alternancia positiva, al calcular el área abajo de la misma se tiene que esta estará dada por:
Vmedio del área = (2/π) * Vmax = 0.636 Vmax.
El valor medio es utilizado en formatos que permiten mejorar el rizo cuando se rectifican corrientes alternas a corriente continua.

El valor medio del área de la alternancia positiva o del pulso será, en cambio:

Si se asume que el área bajo la curva es el trabajo realizado por una corriente senoidal, multiplicando la base por la altura nos daría dicha área, si la curva fuera rectangular, más en este caso, la altura de la curva está dada por el valor pico Vp o valor máximo, pero éste aparece en la curva sólo durante un instante muy breve.
Por lo tanto, el área equivalente en trabajo igual al de la alternancia sería un rectángulo de base igual a la longitud de medio ciclo, que va de 0 a π por una altura que fuera sólo una fracción de Vmax.
A esa fracción se le conoce como VALOR EFICAZ O VALOR RMC (raíz media cuadrática).
Si es un voltaje o corriente se denotan Vrmc o Irmc. Estos factores generan potencias iguales a valores similares de corriente directa continua y se determinan con las fórmulas:


Pingback: Corriente Eléctrica: Qué Es, Tipos, Fórmulas y Cómo Se Mide
Pingback: ¿Qué es el voltaje?